1D Isling Model

We will cover this task during the lab session, and will use a similar implementation for the main problem, the 2D Ising model.

Setup

To keep things simple we pick units so that both \(J\) and \(k_B\) are effectively one. Then the average energy per spin site is \[ \langle E\rangle = - \frac{1}{\text{number of sites}} \frac{1}{2} \sum_{ \begin{array}{c} \text{over all}\\ \text{sites \(i\)} \end{array} } \sum_{ \begin{array}{c} \text{over all}\\ \text{neighbours \(j\)} \end{array} } s_i \cdot s_j \] and the magnetisation per site is \[ \langle M\rangle = \frac{1}{\text{number of sites}} \sum_{ \begin{array}{c} \text{over all}\\ \text{sites \(i\)} \end{array} } s_i \] And the transition probability when flipping to a higher energy state (difference \(\Delta E\)) is \[ p = e^{-\Delta E / T} \]

Initialise model

Implement function 

1
2
def init(n):
    pass

which returns an 1D array of n elements. The each element are -1/+1 with probability 0.5. So a possible output of init(20) is 

1
[ 1 -1 -1  1  1  1 -1  1 -1 -1  1 -1  1 -1  1  1  1  1 -1 -1]

Graphically represent model

Implement function 

1
2
def show(model, title=None, width=None):
    pass

which displays the model using plt.imshow using optional width and title. So a possible output of show(model, title="time = start") is

1D_show
Output of function, show.

Compute energy per spin site

Implement function 

1
2
def energy(model):
    pass

which computes the energy per spin site in model due to spin of neighbouring sites. This function should return values in range -1 (for all spin up) to 1 (all spin down).

Compute bulk magnetisation per spin site

Implement function 

1
2
def magnetization(model):
    pass

which computes the bulk magnetisation per spin site in model. This function should return values in range -1 (for all spin down) to 1 (all spin up). (Note the difference with energy.)

Simulate model

Implement function

1
2
3
def simulate(model, T, t_steps, debug=False):

    return

which performs t_steps Monte Carlo iterations on model. I used the optional parameter debug to print out the usual debug info.

We can now use this function to study the behaviour of the model.

Generate results

Using code like

1
2
3
4
5
6
7
8
rng = default_rng(42)
save_model = init(30)

show(save_model, "Start")
for k in range(6):
    model = save_model.copy()
    simulate(model, 5, 10_000)   
    show(model, "End")

we are able to run a simulation of the same starting state under different conditions.

Low temperature

First when the temperature is low the transition probability limit for a site to flip to a higher state is closer to one so less likely to occur. Hence we expect a trend towards lower energy states

Taking the same initial state:

1D_show

And re-running simulation for 10,000 steps with \(T=0.1\) we get

1D_show 1D_show 1D_show 1D_show 1D_show 1D_show

So system converges to either state where the spins are aligned.

High temperature

Re-running same experiment, using same initial state, for high temperature (\(T=5\)) get

1D_show 1D_show 1D_show 1D_show 1D_show 1D_show

So system don't get alignment of spins and at a local level, the prediction of spins is impossible.

Goldilocks temperature

So what about temperatues that are not too low nor too high?

Re-running same experiment, using same initial state, for temperature (\(T=1\)) get

1D_show 1D_show 1D_show 1D_show 1D_show 1D_show

We get regions of spin alignment. I think the probability distribution of the size of regions is known but I know that I don't know it. These regions are not fixed and "slowly" change over time.

Evolution of magnetisation

Rather than looking at the start and end point we can call the function simulate inside a for loop and compute the magnetisation over time, using code like:

1
2
3
4
5
6
7
T = 5
rng = default_rng(42)
mag = []
model = init(30)
for k in range(1000):
    simulate(model, T, 1)
    mag += [magnetization(model)]
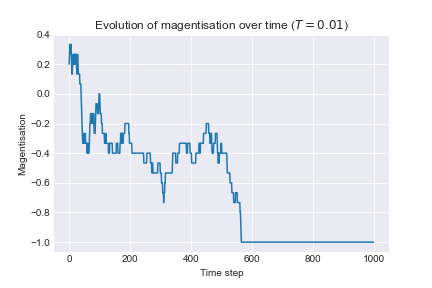
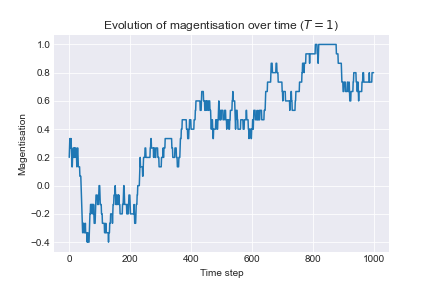
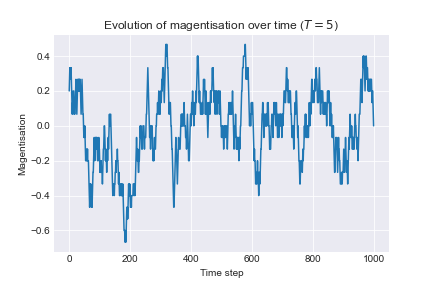
1D_show 1D_show 1D_show
Evolution of magnetisation over time.

Effect of Temperature

To examine the effect of temperature we run the following algorithm:

The corresponding code is 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
points = []

for k in range(400):
    t = rng.uniform(0.001,5)

    model = init(20)
    simulate(model, t, 100_000)

    mag = magnetization(model)
    e = energy(model)

    points.append( (t, e, mag) )

and the resulting plot using 

1
2
3
4
5
6
data = np.array(points)
plt.plot(data.T[0], data.T[2], ".")
plt.title("Phase Transition")
plt.ylabel("Magnetisation")
plt.xlabel("Temperature")
plt.show()
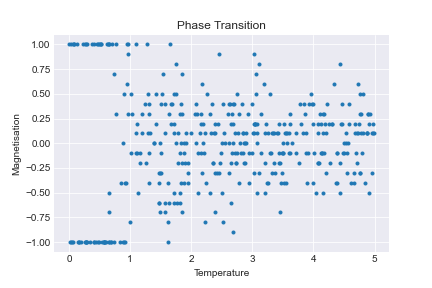
1D_show
Evolution of magnetisation over time.

This is very noisy and difficult to see, so we need to tweak our algorithm by:

The updated code is

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
points = []

for k in range(400):
    t = rng.uniform(0.001,5)

    model = init(20)
    simulate(model, t, 50_000)

    mag = e = 0

    for k in range(100):
        simulate(model, t, 500)
        mag += magnetization(model)
        e += energy(model)

    points.append( (t, e/100, mag/100) )

and the resulting plot is

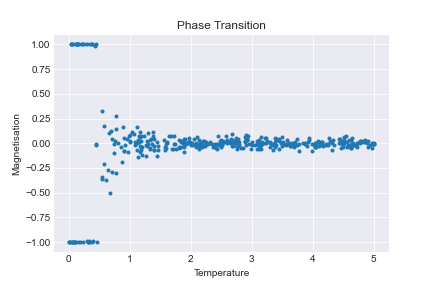
1D_show
Evolution of magnetisation over time.

This is much better. Now we can see that something fundmental happens around \(T=1\), where the model switches from the low temperature state to the high temperature states. This temperature, \(T=1\), is called the critical temperature. We want to determine the corresponding critical temperature for the 2D model.

The corresponding energy plot is

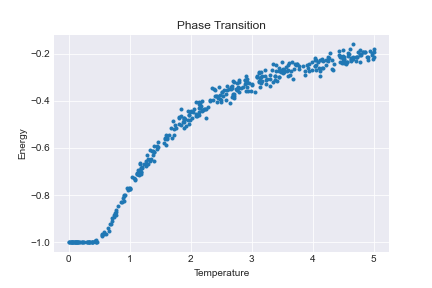
1D_show
Evolution of magnetisation over time.

Comments

There are a number of (optional) improvements that can be made to this implementation. In particular